Klassifizierung der $Z^0$-Ereignisse

Ihre erste Aufgabe in diesem Versuch wird es sein, an Hand von Ereignisdarstellungen auf dem Computerbildschirm und mit Hilfe weniger Messgrößen die verschiedenen $Z^0$-Zerfälle zu identifizieren und von Untergrundereignissen zu unterscheiden. Dieses Kapitel soll Ihnen die wichtigsten Grundlagen dazu vermitteln.

Teilchenidentifikation im OPAL-Detektor

Da wir die Ereignisse nur aufgrund ihrer Endzustände trennen können, ist eine gute Teilchenidentifikation eine wichtige Voraussetzung. Zuerst teilen wir alle Teilchen in geladene (sichtbare Spur in den Spurkammern) und ungeladene ein.

Geladene Teilchen

Geladene Hadronen unterscheiden sich von Elektronen durch die „Form” und den Startpunkt des Schauers, der im elektromagnetischen Kalorimeter (ECAL) ausgelöst wird. Der elektromagnetische Schauer eines Elektrons ist vollständig im ECAL enthalten und hat eine geringe laterale Ausdehnung. Hadronische Schauer dagegen beginnen in der Regel später, sind breiter und dehnen sich in das hadronische Kalorimeter (HCAL) aus. Der Schwerpunkt der Energiedeposition liegt meistens im HCAL. Die Unterschiede von elektromagnetischen und hadronischen Schauern werden jedoch mit fallender Teilchenenergie immer geringer, geladene Hadronen und Elektronen können unterhalb einer Energie von 2 GeV mit Hilfe der Schauerentwicklung nicht mehr getrennt werden. Bei niedrigen Energien besteht die Möglichkeit, Teilchenidentifikationen auf Grund des spezifischen Energieverlusts $dE/dx$ in der Jet-Kammer durchzuführen.

Myonen erzeugen beim Durchgang durch die Kalorimeter keinen Schauer, sie verlieren ( $m_{\mu} >> m_{e}$) auch als minimal ionisierende Teilchen nur wenig Energie durch Ionisation $(dE/dx)$, entsprechend dem Gesetz von Bethe-Bloch, und können daher dicke Materieschichten durchdringen (vgl. Abb. 4.1)

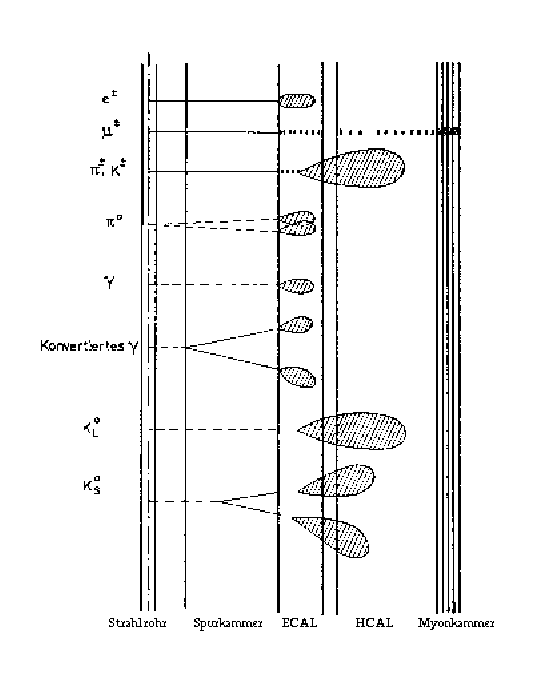
Abbildung 4.1: Schematische Darstellung der Signatur von Elementarteilchen im OPAL-Detektor. Durchgezogene Linien in den Spurkammern deuten Spuren von geladenen Teilchen, gestrichelte Linien „nicht gefundene Spuren” neutraler Teilchen an. Die eingezeichneten „Blasen” zeigen die Umrisse der elektromagnetischen und hadronischen Schauer.

Neutrale Teilchen

Die Identifikation neutraler Teilchen erfolgt über die unterschiedlichen Schauerprofile (Länge, Breite). Neutrale Teilchen, die in den Spurkammern in geladene Teilchen zerfallen bzw. konvertieren, zeigen zwei Spuren mit einer typischen V-Form. Die Spitze des V, also der Zerfallsort des neutralen Teilchens, liegt dabei außerhalb des Primärvertex.

Das $\pi^0$ zerfällt „sofort” in zwei Photonen, deren Öffnungswinkel von der Energie des $\pi^0$ abhängt. Mit steigender Energie liegen die beiden Photonen immer dichter zusammen (Lorentzboost) und können dann von einem einzelnen Photon, das nicht aus einem $\pi^0$-Zerfall stammt, nicht mehr unterschieden werden. Photonen werden durch ihren elektromagnetischen Schauer, neutrale Pionen durch zwei dicht beieinander liegende elektromagnetische Schauer identifiziert. Es darf dabei in beiden Fällen keine Spur gefunden werden, welche auf die Schauer zeigt.

Bevor Photonen in das ECAL eintreten, können sie in Materie in ein $e^+e^-$-Paar konvertieren. Da praktisch die gesamte Materie (oder besser: die gesamte Strahlungslänge) in den Wänden des Zentraldetektors und der Spule konzentriert ist, besteht eine große Wahrscheinlichkeit, dass die Konversion in diesen Bereichen stattfindet. Ein konvertiertes Photon wird durch zwei geladene Spuren in V-Form und durch zwei elektromagnetische Schauer identifiziert. Spuren und Schauer müssen eindeutig zueinander in Beziehung stehen.

Neutrale Hadronen mit großer Fluglänge werden durch einen hadronischen Schauer, auf den keine Spur zeigt, identifiziert. In Abb. 4.1 ist weiterhin der Zerfall eines $K^0_S$ in zwei geladene Pionen als Beispiel für die Signatur eines kurzlebigen neutralen Hadrons gezeigt. Der Zerfall findet mit einem Verzweigungsverhältnis von $\approx$ 69% statt. Nicht gezeigt ist der Zerfall des $K^0_S$ in zwei neutrale Pionen mit einem Verzweigungsverhältnis von $\approx$ 31%.

Messgrößen und Schnitte

Für die im Praktikumsversuch durchzuführende Analyse ist es jedoch weniger wichtig, ein $K^0$ von einem $\pi^0$ zu unterscheiden, als Elektronen und Myonen von Hadronen. Außerdem betrachten wir im zweiten Teil so viele Ereignisse (es wurden ca. 4 000 000 $Z^0$-Zerfälle aufgezeichnet, die Sie jedoch nicht alle bearbeiten), dass wir nicht alle Details wie Schauerform oder spezielle Geometrie betrachten können, sondern diese in globalen Variablen zusammenfassen.

Messgrößen

In Ihrem N-Tupel haben Sie die folgenden Größen zur Verfügung:

• Run: Bezeichnet zeitlich zusammenhängende Messperiode
• Event: Dient zur eindeutigen Identifikation des Ereignisses innerhalb einer Messperiode
• Ncharged: Anzahl der in den Spurkammern gefundenen Spuren geladener Teilchen eines Ereignisses.
• Pcharged: Skalare Summe der in den Vertex-/Jet-/Z-Kammern gemessenen Impulse aller geladenen Spuren eines Ereignisses. ('geladene Energie')
• N_ecal: Anzahl der Einträge ins elektromagnetische Kalorimeter.
  
• E_ecal: Gesamte im ECAL gemessene Energie eines Ereignisses.
  ('ECAL Energie')
• E_hcal: Gesamte im HCAL gemessene Energie eines Ereignisses.
  ('HCAL Energie')
• Nmuonen: Anzahl der in den Myonkammern gefundenen Einträge.
  
• Thrust: $\max_{\theta} \frac{\sum_{i=1}^{NCharged}\vec{p_i}\cdot\vec{n}(\theta,\phi)} {\sum_{i=1}^{NCharged}\vert\vec{p_i}\vert}$, wobei $\vec{n}(\theta,\phi)$ eine beliebige Achse durch den Vertex ist. Die Achse $\vec{n}(\theta,\phi)$, bei der das Maximum auftritt wird auch als Thrustachse bezeichnet. Diese Größe gibt an, wie weit gefächert der Teilchenstrahl ist. Die Thrustachse entspricht meistens ungefähr der Achse, auf der das primär erzeugte Fermion-Antifermionpaar auseinander geflogen ist. Sie ist durch die Winkel $\theta$ und $\phi$ definiert.
• Cos_thru: Cosinus des Winkels $\theta$ (Winkel zwischen Thrust- und Strahlachse). Gibt die Lage der Ereignisachse zum Strahlrohr an
• C_thru_n und C_thru_p: Cosinus des Winkels $\theta$, wenn man separate Thrustachsen für die von Fermion und Antifermion erzeugten Teilchenjets bildet.
• Acol: Die Acolinearität ist der Winkel zwischen thru_n und thru_p
• Phi_thru: Winkel $\phi$ der Thrustachse
• D0mean: Mittlerer Abstand aller Spuren von der Detektormitte in der $r-\phi$-Ebene in cm
• Z0mean: Mittlere z-Koordinate aller Spuren in cm
• E_lep: Strahlenergie, d.h. halbe Schwerpunktsenergie

Dabei sind alle Energien in GeV angegeben.

In welcher Weise diese Messgrößen eingesetzt werden, wird im folgenden Abschnitt detailliert erläutert. Als Beispiel kann die Trennung der $Z^0\rightarrow e^+e^-$-Ereignisse von $Z^0\rightarrow \mu^+ \mu^-$-Ereignissen erste Erkenntnisse liefern. Beide Ereignisklassen unterscheiden sich, wie man sich leicht überlegen kann, fast nicht in den Variablen Pcharged und Ncharged. Kleine Unterschiede werden wegen der in $e^+e^- \rightarrow e^+e^-$-Ereignissen größeren Wahrscheinlichkeit, Bremsstrahlungsphotonen abzugeben, verursacht. Große Unterschiede ergeben sich aber in der totalen Energie im ECAL. Für die $e^+e^- \rightarrow e^+e^-$ - Ereignisse sollte im Mittel die Schwerpunktsenergie gemessen werden. In den $e^+e^- \rightarrow \mu ^+ \mu ^-$-Ereignissen erwartet man von den beiden Myonen, wie bereits erwähnt, nur eine kleine Energiedeposition mit einem Äquivalent von $\approx$ 2 GeV im ECAL. In $e^+e^- \rightarrow e^+e^-$-Ereignissen wird keine Energie im HCAL deponiert. Die Myonen der $e^+e^- \rightarrow \mu ^+ \mu ^-$-Ereignisse durchdringen das ECAL und das HCAL und geben zusammen im Mittel ein Energieäquivalent von $\approx$ 5 GeV an das HCAL ab. Die Trennung der $e^+e^- \rightarrow e^+e^-$-Ereignisse von den $e^+e^- \rightarrow \mu ^+ \mu ^-$-Ereignissen kann also mit einem sogenannten Schnitt auf die Messgröße E_ecal durchgeführt werden. Man verlangt, dass E_ecal größer sein muss als ein bestimmter, vom Experimentator ($\equiv$ Praktikumsteilnehmer) zu ermittelnder Wert.

Akzeptanz und Untergrund

Das Ziel ist es, den Schnitt in einer geeigneten Messgröße oder gleichzeitige Schnitte in verschiedenen Messgrößen so zu wählen, dass ein möglichst großer Anteil der „gewünschten” Ereignisse die Schnittbedingung(en) erfüllt und der Anteil an „unerwünschten” Untergrundereignissen möglichst klein wird. Als Akzeptanz einer oder mehrerer Schnitte bezeichnet man das Verhältnis der Ereignisse einer ausgewählten Klasse, welche die Schnittbedingungen passieren, zu der Zahl aller vorhandener Ereignisse derselben Klasse. Die erreichte Akzeptanz und Untergrundunterdrückung hängen sowohl von den Mittelwerten als auch von den Breiten der Verteilungen ab. Dazu sind in Abb. 4.2 zwei hypothetische Beispiele gezeigt.

Abbildung 4.2: Beispiele zur Prozedur des Schneidens

Im ersten Beispiel sind die Ereignisklassen A und B in der Variablen X vollständig getrennt. Eine Akzeptanz von 100% und eine vollständige Unterdrückung der jeweils unerwünschten Ereignisklasse ist mit einem Schnitt zwischen 40-60 in der Variablen X möglich. Dies ist der Idealfall. Der Normalfall ist im zweiten Beispiel gezeigt. Mit der Wahl des Schnitts legt man die Akzeptanz und die Beimischung des Untergrunds fest. Liegt das Augenmerk darauf, eine besonders reine Menge der Ereignisklasse A zu erhalten, muss der Schnitt in X klein gewählt werden ( $X < 20 - X < 40$). Will man möglichst alle Ereignisse der Klasse A behalten, so muss der Schnitt groß gewählt werden ( $X < 40 - X < 60$).

Um eine Ereignisklasse aus den gesamten Daten abzutrennen, genügt es meistens nicht, nur in einer Messgröße zu schneiden; es sind gleichzeitige Schnitte in verschiedenen Messgrößen erforderlich. Weiterhin können Schnitte natürlich auch auf zusammengesetzte Messgrößen erfolgen. Fordert man z.B. $X^2 + Y^2 < A$, so schneidet man im zweidimensionalen Raum X-Y eine Kreisfläche mit dem Radius $\sqrt{A}$ aus. Das Ziel dieses Schnittverfahrens ist es, die am besten geeigneten Variablen zu finden und die Schnittbedingungen zu optimieren, um eine möglichst reine Ereignismenge zu erhalten.

Im Praktikumsversuch müssen diese Schnitte von Hand gemacht werden, es ist jedoch auch möglich, mathematische Optimierungsverfahren (Fischer Diskriminanten, neuronale Netze) zu nutzen. Wendet man diese Verfahren an, so ist es jedoch schwieriger, systematische Fehler zu bestimmen.

Ereignissimulation (Monte-Carlo)

Durch Schnitte verliert man prinzipiell, wie es in Abb. 4.2 anschaulich gezeigt ist, Ereignisse der gesuchten Klasse und behält einen Anteil an unerwünschten Untergrundereignissen. Zur Berechnung von Wirkungsquerschnitten (dies ist ebenfalls Teil des Praktikumsversuchs) benötigt man neben der integrierten Luminosität (vgl. Tabelle A) die „genaue” Zahl der aufgetretenen Ereignisse $N$ einer Klasse. Nach den Schnitten erhält man eine Zahl von beobachteten Ereignissen $N_{beob}$, die korrigiert werden muss. Eine Korrektur von $N_{beob}$, die nur auf Daten basiert, ist in Beispiel 2 Abb. 4.2 nicht möglich, da man im Experiment die Verteilungen in der Messgröße X der beiden Ereignisklassen A und B nicht einzeln messen kann, sondern nur deren Summe.

Eine Möglichkeit, die wegen der Schnitte auftretenden Akzeptanzverluste zu bestimmen, bieten Ereignissimulationen mit Hilfe von Computerprogrammen. Dazu wird eine bestimmte, möglichst große Anzahl an Ereignissen einer bestimmten Klasse folgendermaßen generiert: Zunächst erzeugt man in einer $e^+e^-$-Annihilation auslaufende Fermion-Antifermion-Paare. Dann simuliert man für Quark-Antiquark-Paare den Hadronisierungsprozess und dann den Zerfall der instabilen Teilchen. In einem letzten, sehr aufwendigen Schritt werden alle Detektorsignale simuliert, wie sie von den durchlaufenden Teilchen erzeugt werden, so dass zum Schluss die Informationen in gleicher Weise vorliegen wie bei „richtigen” Ereignissen. Simulierte und beobachtete Ereignisse können jetzt mit den gleichen Analyseprogrammen untersucht werden. Bei der Ereignissimulation werden alle nutzbaren theoretischen und experimentellen Kenntnisse verwendet. Die simulierten Daten enthalten neben den auch in tatsächlichen Daten enthaltenen Informationen zusätzlich Angaben über die entstandenen Teilchen, so dass man die Reaktion des Detektors bei ganz bestimmten Ereignissen untersuchen kann!

Simuliert man in unserem Beispiel die Ereignisklassen A und B, so können die einzelnen Verteilungen in der Größe X getrennt bestimmt werden. Wendet man nun die gleichen Schnitte wie auf die Daten an, so erhält man sehr einfach die Akzeptanz. In gleicher Weise kann man den Untergrundbeitrag berechnen. Dazu ist allerdings eine relative Normierung zwischen den beiden Verteilungen der Klasse A und B nötig. Dies kann z.B. durch eine Anpassung der Daten an die beiden überlagerten Einzelverteilungen erfolgen. Das Ergebnis der Anpassung ist dann der relative Anteil an Ereignissen der Klasse A zur Klasse B.

Man sollte jedoch bei der Verwendung von Monte-Carlos nie aus den Augen verlieren, dass man bereits eine Menge Annahmen über den zu untersuchenden Prozess in die Auswertung hineinsteckt. Man muss also aufpassen, dass die Ergebnisse nicht zu stark mit den Monte-Carlos korreliert sind, sonst bekommt man nur das Ergebnis, das man hineingesteckt hat. So können systematische Fehler entstehen, deren Beurteilung für Sie jedoch schwierig ist (da Sie nichts über die Entstehung der Monte-Carlos wissen) und über den Praktikumsversuch hinaus geht.

Selektion der $Z^0$-Ereignisse

$e^+e^- \rightarrow \nu \bar {\nu }$

Die Zerfallsprodukte dieses Zerfalls können nicht nachgewiesen werden, man spricht deshalb von den sogenannten “invisible decay modes”. Es besteht allerdings die Möglichkeit, den Zerfall $Z^0\to\nu\bar{\nu}$ zu identifizieren, indem man das Anfangsbremsstrahlungsphoton der Reaktion $e^+e^-\to\gamma\nu\bar{\nu}$ nachweist.

$e^+e^- \rightarrow e^+e^-$

Abbildung 4.3: GROPE Bild $e^+e^- \rightarrow e^+e^-$

Es sind in niedrigster Ordnung der Störungstheorie drei Prozesse (Feynman-Graphen) von Bedeutung (Abb. 4.8a,b,c). Betrachtet man nur den s-Kanal-Austausch des $Z^0$ und des Photons, so ist bei einer Schwerpunktsenergie, die der zentralen Masse des $Z^0$ entspricht, der Photonaustausch um zwei Größenordnungen und der Interferenzterm um drei Größenordnungen unterdrückt. Eine wichtige Rolle spielt jedoch der t-Kanal-Austausch des Photons, wie er in Abb. 4.8c gezeigt ist. Dieser Prozess hat einen sehr hohen Wirkungsquerschnitt für kleine Streuwinkel ($\Theta$) und wird wegen der genauen Kenntnis des Wirkungsquerschnittes benutzt, um die Luminosität zu messen. Um t- und s-Kanal voneinander zu trennen, steht Ihnen im Versuch das Notebook 02_s_channel.ipynb zur Verfügung.

$e^+e^- \rightarrow \mu ^+ \mu ^-$

Abbildung 4.4: GROPE Bild $e^+e^- \rightarrow \mu ^+ \mu ^-$

Diese Ereignisklasse wird durch zwei das HCAL durchdringende Myonen und durch Signale in den Myonkammern identifiziert. Die Spurpunkte in den Myonkammern müssen eindeutig mit den Spuren im Zentraldetektor in Verbindung gebracht werden. Bei der Extrapolation der Zentraldetektorspur muss auch das Magnetfeld im HCAL berücksichtigt werden. Das Übereinstimmen lässt sich jedoch nur in den Orginaldaten und nicht in den N-Tupeln prüfen. Daher ist es besser, den Impuls der Spuren (ziemlich genau 90 GeV) als Schnittgröße herzunehmen.

$e^+e^- \rightarrow \tau ^+ \tau ^-$

Abbildung 4.5: GROPE Bild $e^+e^- \rightarrow \tau ^+ \tau ^-$

Das Tau-Lepton kann in viele verschiedene Endzustände zerfallen (vgl. Tabelle 4.3.4). Eine Zuordnung zu einem bestimmten Zerfallskanal kann daher im Rahmen des Praktikums nicht durchgeführt werden.

Man unterscheidet Tau-Zerfälle oft nach der Zahl der emittierten geladenen Teilchen und spricht von n-prong-Ereignissen, wenn das Tau in n geladene Teilchen zerfällt. Dabei überwiegen bei weitem die 1-prong-Zerfälle (1-prong: $\approx$ 86%, 3-prong: $\approx$ 14%, 5-prong: $\approx$ 0.11%). Um $\tau^+ \tau^-$-Ereignisse gegen hadronische Ereignisse abzutrennen, verlangt man, dass die geladene Multiplizität klein ist. Mit diesem Schnitt hat man jedoch noch keine Unterscheidung in den leptonischen Ereignissen gefunden. Das in jedem Tau-Zerfall emittierte Neutrino trägt einen Teil der Energie mit sich, ohne dass es im Detektor nachgewiesen wird. Verlangt man deshalb, dass die „ECAL Energie” deutlich kleiner ist als die Schwerpunktsenergie, so kann man $\tau^+ \tau^-$-Ereignisse bereits sehr gut von $e^+e^-$-Ereignissen trennen.

Tabelle: Die Zerfallsmodi des Tau-Leptons mit den größten Verzweigungsverhältnissen am Beispiel des $\tau ^-$-Zerfalls.

Zerfallsmodus	Verzweigungsverhältnis
$\pi^- \pi^0 \nu_{\tau}$	25.51% $\pm$ 0.09%	1-prong
$e^- \bar{\nu}_e \nu_{\tau}$	17.85% $\pm$ 0.05%	1-prong
$\mu^- \bar{\nu}_{\mu} \nu_{\tau}$	17.36% $\pm$ 0.05%	1-prong
$\pi^- \nu_{\tau}$	10.91% $\pm$ 0.07%	1-prong
$\pi^- \pi^- \pi^+ \nu_{\tau}$	9.32% $\pm$ 0.07%	3-prong
$\pi^- \pi^- \pi^+ \pi^0 \nu_{\tau}$	4.61% $\pm$ 0.06%	3-prong
$\pi^- \pi^0 \pi^0 \pi^0 \nu_{\tau}$	1.04% $\pm$ 0.07%	1-prong

In gleicher Weise kann man gegen $\mu^+ \mu^-$-Ereignisse schneiden, indem man fordert, dass die „geladene Energie” kleiner als die Schwerpunktsenergie ist. Es sind eine ganze Reihe weiterer Schnitte zur Identifikation des Tau-Leptons entwickelt worden, die z.B. ganz bestimmte Zerfallskanäle herausfiltern.

$e^+e^- \rightarrow q \bar {q}$

Abbildung 4.6: GROPE Bild $e^+e^- \rightarrow q \bar {q}$

Die mittlere gemessene Multiplizität (Zahl der rekonstruierbaren, geladenen Spuren) in hadronischen Ereignissen beträgt $\approx$ 20 und ist damit sehr viel größer als in leptonischen Ereignissen. Zusätzlich werden in dem Hadronisierungsprozess des Quark-Antiquark-Paares neutrale Hadronen, hauptsächlich $\pi^0$, erzeugt. Hadronische Ereignisse sind mit einem Schnitt in der Multiplizität im Prinzip leicht von allen übrigen Ereignissen zu trennen. Man muss prinzipiell die bisher nicht erwähnten Zwei-Photon-Reaktionen als Untergrundquelle in Betracht ziehen, ein Beispiel für diesen Prozess ist in Abb. 4.8e gezeigt. Elektron und Positron strahlen jeweils ein virtuelles Bremsstrahlungsphoton ab, welche sich in einem Fermion-Antifermion-Paar ($f\bar{f}$) vernichten. Handelt es sich dabei um Quark-Antiquark-Paare, so hadronisieren diese wiederum in beobachtbare Teilchen. Elektron und Positron werden meist nur wenig gestreut und bleiben in der Vakuumröhre oder treffen auf den Forward Detektor (FCAL). Damit erhält man ein Ereignis mit vergleichsweise hoher Multiplizität. Die totale Energie ist in diesen Ereignissen allerdings klein, so dass man nach einem zusätzlichen Energieschnitt praktisch nur noch hadronische Ereignisse übrig behält.

Wichtige Hinweise zur Selektion

Die hier diskutierten Effekte sollten eine direkte Auswirkung auf Ihre Selektion haben:

1. Leptonische Ereignisse haben bei kleinen Streuwinkeln oft so wenige Hits in der Spurkammer, dass sich zwar eine Spur rekonstruieren lässt, der Impuls jedoch sehr ungenau ist. Daher ist es sinnvoll, bei leptonischen Ereignissen auf $-0.9<Cos\_thru<0.9$ zu schneiden.
2. Die kosmischen Myonen stellen eine wichtige Untergrundquelle dar (überlegen Sie sich, in welchen Zerfallskanälen). Sie entstehen durch Wechselwirkungen der kosmischen Strahlung mit der Atmosphäre. Sie können die Tatsache ausnutzen, dass die Spuren von kosmischen Myonen nicht nur von der Detektormitte kommen, sondern gleichmäßig über den Detektor verteilt sind. Dazu stehen Ihnen die Größen D0mean und Z0mean zur Verfügung.

   Abbildung: Unterschied zwischen Myonen aus $Z^0$-Zerfällen (links) und kosmischen Myonen (rechts) bei Betrachtung mit starkem Zoom

   
3. Eine weitere Untergrundquelle sind die bereits angesprochenen 2-Photon-Ereignisse, die sich besonders bei den $\tau$- und Hadron-Ereignissen bemerkbar machen. Hier empfiehlt sich ein Schnitt auf die Acolinearität, da die beiden abgestrahlten Photonen meist nicht die gleiche Energie haben und das Ereignis somit entlang der z-Achse geboostet ist.
4. Geladene Teilchen können Bremsstrahlung emittieren. Man unterscheidet die sogenannte “initial state radiation (ISR)” , d.h. Bremsstrahlung, bei der die einlaufenden Elektronen (Positronen) Photonen emittieren, und die “final state radiation (FSR)”, d.h. Bremsstrahlung durch die geladenen Teilchen im Endzustand. Ein ISR-Photon geht meistens entlang der Strahlröhre und ist somit meist nicht sichtbar. Der Impuls des Photons macht sich durch einen “boost” bemerkbar, da das CM-System von $e^+$ und $e^-$ nicht mehr das Laborsystem ist. Auch die FSR trägt dazu bei, dass bei einigen Ereignissen sowohl Impuls- als auch Energiesumme geringer sind, als man es erwarten würde. Dies ist insbesondere bei Elektron-Ereignissen unangenehm, da man hier einen Schnitt auf die geladene Energie machen möchte, um sie von den Tau-Ereignissen zu trennen.

Abbildung 4.8: Feynman-Diagramme der wichtigsten untersuchten Prozesse

Allgemeine Hinweise zur Teilchenidentifikation

Abschließend diskutieren wir Effekte, die alle Zerfallskanäle des $Z^0$ gleichermaßen betreffen. Sie sind zwar für die Durchführung des Praktikumsversuches nicht bedeutsam, vermitteln jedoch einen Ausblick, was bei einer genaueren Analyse noch beachtet werden muss.

1. Elektronisches Rauschen, das den Signalen der Detektoren überlagert ist, kann ein Signal vortäuschen und zu Fehlinterpretationen führen. Zum Beispiel findet man in der Jet-Kammer einzelne isolierte Spurpunkte, die nicht mit einer Spur assoziiert werden können. Durch elektronisches Rauschen kann auch eine kleine Energiedeposition in den Kalorimetern vorgetäuscht werden. Deshalb können Photonen unterhalb einer Energie von $\approx$ 1 GeV nicht mehr eindeutig nachgewiesen werden.
2. Die Nachweiswahrscheinlichkeit aller Detektorkomponenten ist immer kleiner als 100%. So kann es z.B. vorkommen, dass in den Myonkammern nur 3 der 4 Lagen ein Signal erzeugen. Ebenso können in einer ansonsten gut zu identifizierenden Spur in der Jet-Kammer ein oder mehrere Spurpunkte fehlen.
3. Bedingt durch den Aufbau der Detektoren, ergeben sich Lücken zwischen den einzelnen Modulen der Kalorimeter und im Vorwärts-Rückwärts-Bereich (Durchführung des Strahlrohres). Treffen Teilchen auf diese Lücken, so erhält man falsch gemessene Energien. Bei geladenen Teilchen kann man die Spur durch die Kalorimeter extrapolieren, um festzustellen, ob eine Lücke getroffen wurde.
4. Ein wichtiger Aspekt für die Teilchenidentifikation von Elektronen, Myonen und besonders von Tau-Leptonen, welche aus den leptonischen Zerfällen des $Z^0$ stammen, ist die Redundanz, die man durch die paarweise Produktion von Teilchen und Antiteilchen erhält. Wurde z.B. ein $\tau ^-$-Lepton aus dem Zerfall des $Z^0$ eindeutig nachgewiesen, so muss in diesem Ereignis auch ein $\tau^+$-Lepton vorhanden sein. Damit lassen sich die zur Identifikation benutzten Kriterien auf einfache Weise testen und die Nachweiswahrscheinlichkeit berechnen.
5. Eine Untergrundquelle sind die sogenannten „beam-gas”-Ereignisse. Dies sind Streuungen von Elektronen oder Positronen des Strahls mit Teilchen des Restgases in der Vakuumröhre. Sie unterscheiden sich unter anderem von $e^+e^- \rightarrow e^+e^-$-Wechselwirkungen durch die Vertexposition, die außerhalb der Detektormitte liegen kann, und dadurch, dass praktisch alle Teilchen entweder in Vorwärts- oder in Rückwärtsrichtung fliegen.